Optimising SETS for Fusion

I can’t remember the last time I’ve been this pleased with an algorithm.

SETS has delivered shorter and easier-to-read code, a tidy 30-40% speedup that scales even better for larger graphs, and better unit test conformance, fixing some of the most evasive and hard-to-reproduce Fusion bugs I’ve ever had to deal with - all of this with a turnaround time of under 24 hours to go from original idea to complete implementation.

I outlined the basics of the algorithm yesterday. Today I’m going to quickly run through the changes and benefits of the algorithm as applied to Fusion.

From naïve to optimised

The original (naïve) implementation of SETS looked very similar to what I put forward in the original blog post. This was never intended to be permanent; instead, I was testing the viability of the algorithm and seeing if it could pass all of the unit tests.

local function updateAll(root: PubTypes.Dependency)
	local counters = {}
	local flags = {}
	local queue = {}

	-- Pass 1: counting up
	for object in root.dependentSet do
		table.insert(queue, object)
	end
	while #queue > 0 do
		local next = table.remove(queue, 1)
		counters[next] = (counters[next] or 0) + 1
		for object in next.dependentSet do
			table.insert(queue, object)
		end
	end

	-- Pass 2: counting down + processing
	for object in root.dependentSet do
		table.insert(queue, object)
		flags[object] = true
	end
	while #queue > 0 do
		local next = table.remove(queue, 1)
		counters[next] -= 1
		local setFlag = false
		if counters[next] == 0 and flags[next] then
			setFlag = next:update()
		end
		for object in next.dependentSet do
			table.insert(queue, object)
			if setFlag then
				flags[object] = true
			end
		end
	end
end

It was trivial to optimise this. Both passes iterate over the same objects in the same order by design, so instead of taking objects out of the queue for processing, we can preserve them and simply walk up the queue ourselves. That way, we can eliminate the expensive calls to table.remove(queue, 1), and the second pass no longer has to do any table processing at all.

local function updateAll(root: PubTypes.Dependency)
	local counters = {}
	local flags = {}
	local queue = {}
	local queuePos = 1

	-- Pass 1: counting up
	for object in root.dependentSet do
		table.insert(queue, object)
	end
	while #queue > 0 do
		local next = queue[queuePos]
		counters[next] = (counters[next] or 0) + 1
		for object in next.dependentSet do
			table.insert(queue, object)
		end
        queuePos += 1
	end

	-- Pass 2: counting down + processing
	for object in root.dependentSet do
		flags[object] = true
	end
    queuePos = 1
	while #queue > 0 do
		local next = queue[queuePos]
		counters[next] -= 1
		local setFlag = false
		if counters[next] == 0 and flags[next] then
			setFlag = next:update()
		end
		for object in next.dependentSet do
			if setFlag then
				flags[object] = true
			end
		end
        queuePos += 1
	end
end

From here, it’s standard optimisation territory. We can move the flag initialisation into the first for loop, and store the size of the queue ourselves so we don’t need to use table.insert or the # operator. In the second pass, we can reverse the order of the if setFlag and for loop, then merge it with the if block above to eliminate the setFlag variable altogether. We can also deduplicate table accesses using variables, and finally add some type annotations to get it to pass strict typing:

local function updateAll(root: PubTypes.Dependency)
	local counters: {[Descendant]: number} = {}
	local flags: {[Descendant]: boolean} = {}
	local queue: {Descendant} = {}
	local queueSize = 0
	local queuePos = 1

	for object in root.dependentSet do
		queueSize += 1
		queue[queueSize] = object
		flags[object] = true
	end

	-- Pass 1: counting up
	while queuePos <= queueSize do
		local next = queue[queuePos]
		local counter = counters[next]
		counters[next] = if counter == nil then 1 else counter + 1
		if (next :: any).dependentSet ~= nil then
			for object in (next :: any).dependentSet do
				queueSize += 1
				queue[queueSize] = object
			end
		end
		queuePos += 1
	end

	-- Pass 2: counting down + processing
	queuePos = 1
	while queuePos <= queueSize do
		local next = queue[queuePos]
		local counter = counters[next] - 1
		counters[next] = counter
		if counter == 0 and flags[next] and next:update() and (next :: any).dependentSet ~= nil then
			for object in (next :: any).dependentSet do
				flags[object] = true
			end
		end
		queuePos += 1
	end
end

Outcomes

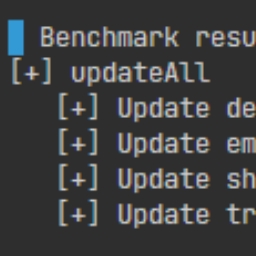
Before I applied SETS, here’s how the above updateAll function performed with its previous implementation. The benchmarks are pretty basic - we’re just running sample code snippets around half a million times and averaging the run time across all of them to get the average execution time of a single run.

Benchmark results:
[+] updateAll
   [+] Update deep tree ......................... 1.99μs
   [+] Update empty tree ........................ 0.28μs
   [+] Update shallow tree ...................... 1.60μs
   [+] Update tree with complex dependencies .... 2.92μs

After merging in SETS, the numbers mostly improved, which was a welcome result:

Benchmark results:
[+] updateAll
   [+] Update deep tree ......................... 1.43μs
   [+] Update empty tree ........................ 0.13μs
   [+] Update shallow tree ...................... 1.64μs
   [+] Update tree with complex dependencies .... 2.24μs

From my limited time playing around with SETS in Fusion, it seems to scale much better for larger graphs of objects, which is awesome. It also fixed the gnarly issues me and Zack came across yesterday, which is great news.

Now that we’ve implemented SETS, we’re pretty much code-ready to launch Fusion v0.2. Unless there are any other concerning bugs, the plan is to finish up the supporting material (docs, examples, etc), fix Wally, and go live.