I don’t know if this has algorithm has a name already, but a cursory glance at Wikipedia says no. So I’m going to call it subgraph-eliminating topological search (SETS) because I like naming things and I’m too lazy to wade through papers.

Motivation

In my reactive library, Fusion, objects can depend on other objects acyclically (without loops). Each object stores a dependent set - a set of the objects that depend on this one.

An object can broadcast an update. In Fusion, this normally means the object has recalculated its value, so anyone dependent on that object’s value should also recalculate their value.

Objects should only recalculate after the objects they depend on; otherwise the object wouldn’t receive the correct, up-to-date values it needs.

Objects should only recalculate once, because performing the same calculation multiple times is wasteful.

If, once an object recalculates, its value is still equal to what it used to be, we don’t need to recalculate objects using that value, because performing those calculations with the same value as before is wasteful.

Is it possible to efficiently iterate over the objects and update them in the correct order, calculating each only once, and eliminating objects that don’t need to be recalculated again?

Topological sort - route counting

Before we get to SETS, let’s start by considering a simpler topological sorting algorithm.

Topological sorting is a way of arranging objects in a list, so the dependents of any object appear strictly after the object itself. This is useful across a wide variety of computing tasks, for example scheduling tasks to run only after previous tasks have calculated required results. Even Fusion has used toposort before, to make sure objects update in the correct order.

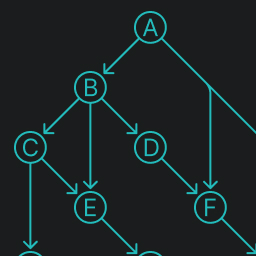
Before we start, we should arrange our objects in a graph, with directed edges flowing from ancestors to descendants. Make sure it does not include any cycles - you will end up with a directed acyclic graph (cool kids call them DAGs).

Instead of taking the usual approaches to topological sorting that the internet seems to suggest, I’m going to use a counting approach. To put it simply, we’re going to count how many different ways you can arrive at each object by taking different routes through the graph.

Give every object a counter that starts at 0, and create a queue of objects. Fill the queue with A’s direct descendants on the graph. Now, repeat this until the queue is empty:

1. Take the first object out of the queue.
2. Add one to the object’s counter.
3. Push all of the object’s direct descendants onto the end of the queue.

This is essentially a breadth-first search of the graph, where we add one to every object we find. By the end, you’ll have a graph labelled like this:

Some objects are visited multiple times in this algorithm. That reflects the fact that our algorithm takes multiple routes to explore the entire graph. As a consequence of this, every object ends up counting how many routes you can take to arrive at that object. For example, Object I (on the far right) has three unique routes preceding it:

Some of these routes are more long-winded compared to others. Therefore, it should make reasonable sense that the longest route will arrive at the object last, performing the final addition on the counter. There will be no other route leading into the object after that, so we can safely say all of the routes have been covered. That’s an important observation.

Now that we’ve counted the routes to all of our objects, let’s now do the inverse; explore the graph in the same way, but this time count back down to zero. For any given object, it will only reach zero when all routes leading up to it have been explored, for the same reasons as given above. That means the objects must hit zero in topological order, because an object can’t hit zero until all the objects before it have been explored.

We can take advantage of that fact to write a neat little topological sorting algorithm, which takes in a starting object (the ‘root’ of the graph) and returns all following objects in topological order.

-- This is a naïve implementation, but if you use it, linking back to this blog
-- post would be much appreciated. Thank you <3
local function toposort(root)
    local counters = {}
    local queue = {}
    local sorted = {}

    -- Pass 1: counting up
    for object in root.descendants do
        table.insert(queue, object)
    end
    while #queue > 0 do
        local next = table.remove(queue, 1)
        counters[next] = (counters[next] or 0) + 1
        for object in next.descendants do
            table.insert(queue, object)
        end
    end

    -- Pass 2: counting down + processing
    for object in root.descendants do
        table.insert(queue, object)
    end
    while #queue > 0 do
        local next = table.remove(queue, 1)
        counters[next] -= 1
        if counters[next] == 0 then
            table.insert(sorted, next)
        end
        for object in next.descendants do
            table.insert(queue, object)
        end
    end

    return sorted
end

It’s worth taking the time to understand what’s going on here. This simplified route counting method forms the basis of the more powerful SETS algorithm.

Introducing SETS

SETS is a simple algorithm which allows for any directed acyclic graph of objects to be processed in topological order, while also allowing for irrelevant subgraphs to be eliminated from being processed. In plain English, that means it will make sure our objects are processed in the right order, while also allowing us to skip objects we don’t need to process.

The only things you need for SETS to work is:

• one-way connections from ancestor to descendant objects
• one (unsigned) integer counter and boolean flag per object
• a queue to hold objects currently being processed

SETS works in two passes. The first pass counts up the number of routes you can take to reach each object. The second pass counts back down, processing objects as each counter hits zero. By passing flags down, you can then control which objects to process and which objects to skip, allowing you to eliminate entire sections of the graph if you don’t deem them useful.

To line up with our original Fusion motivation, let’s say we’re processing the objects in the graph by recalculating their value. If the new value is the same as before, then we want to skip processing the descendants of that object. You need to be careful though, because if some of those descendants are accessible by another route, they’ll still need to be processed.

The way we will approach this is by giving every object an additional ‘flag’ boolean, in addition to the existing integer counter. This flag will indicate if an ‘active’ route has reached the object. When we’re processing objects on the way down, if we don’t want to skip the object, then we’ll pass the flag down to the next few descendants of the object. Otherwise, the flag won’t be passed down, but we’ll still traverse the descendants to do the route counting. The flag then becomes an easy way to tell whether an object has been skipped; we don’t need to process objects without the flag set.

You’ll need to remember to set the flags for the first objects you add to the queue, because otherwise they’ll be skipped and you won’t process anything.

A naïve implementation of the SETS algorithm might look like this:

-- This is a naïve implementation, but if you use it, linking back to this blog
-- post would be much appreciated. Thank you <3
-- `process` is a callback that returns false when the processed object's
-- descendants should be skipped.
local function sets_search(root, process)
    local counters = {}
    local flags = {}
    local queue = {}

    -- Pass 1: counting up
    for object in root.descendants do
        table.insert(queue, object)
    end
    while #queue > 0 do
        local next = table.remove(queue, 1)
        counters[next] = (counters[next] or 0) + 1
        for object in next.descendants do
            table.insert(queue, object)
        end
    end

    -- Pass 2: counting down + processing
    for object in root.descendants do
        table.insert(queue, object)
        flags[object] = true
    end
    while #queue > 0 do
        local next = table.remove(queue, 1)
        counters[next] -= 1
        local setFlag = false
        if counters[next] == 0 and flags[next] then
            setFlag = process(next)
        end
        for object in next.descendants do
            table.insert(queue, object)
            if setFlag then
                flags[object] = true
            end
        end
    end
end

As you can probably tell, this looks similar to the toposort algorithm we had before. The thing that’s new here is the subgraph elimination - it’s ergonomic and efficient to skip over computations for parts of the graph you don’t need, while preserving the order of the rest of your computations the same relative to each other.

Closing thoughts

I came up with this algorithm independently while diagnosing an issue with Fusion’s existing toposort during my day job. Me and Zack had noticed our button tooltips were getting into completely wacky, impossible states. Upon closer inspection I found some nasty edge cases in the previous toposort approach, and decided to try and find a proper algorithm to process our reactive objects.

It’s such a shame that we’re considering moving to a different evaluation model, where we probably won’t need an algorithm like this. It’s still neat though.